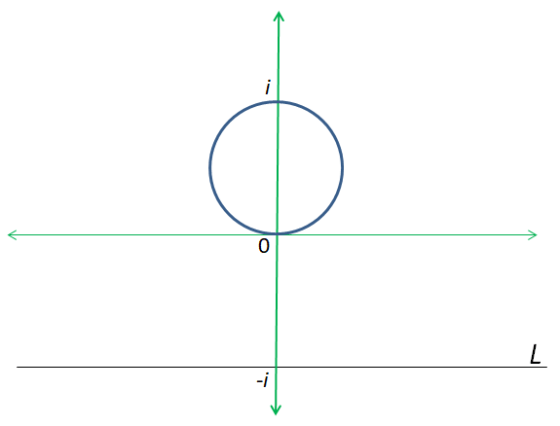
Saya telah memperkenalkan fungsi kompleks dan memberikan contoh fungsi kompleks Fungsi ini memetakan lingkaran satuan ke lingkaran satuan lagi. Persisnya,…
Fungsi Kompleks
Misal Fungsi yang memetakan setiap bilangan ke bilangan disebut fungsi kompleks. Perhatikan jika dipetakan ke maka dan merupakan fungsi dari…
Akar i
Bila akar 1 adalah dan akar adalah lalu akar sama dengan apa? Bagaimana mencarinya? Untuk mendapatkan akar tuliskan persamaan dalam…
Akar -1
Dalam sistem bilangan kompleks, akar adalah bilangan kompleks yang memenuhi persamaan yaitu Bilangan dalam hal ini merupakan akar utama (dari)…
Akar 1
Di akar 1 (yakni, bilangan real yang memenuhi persamaan ) ada dua, yaitu 1 dan Akar utama dari 1 disepakati…
Bilangan Kompleks dalam Bentuk Polar
Bilangan kompleks dapat dinyatakan dalam bentuk polar dengan dan (bila ). Bentuk ini dikenal sebagai rumus Euler untuk bilangan kompleks.…
Bilangan Kompleks sebagai Matriks
Bila Anda merasa penyajian bilangan kompleks sebagai pasangan bilangan, dengan rumus penjumlahan dan perkalian yang saya perkenalkan dalam artikel sebelumnya,…
Bilangan Kompleks sebagai Pasangan Bilangan
Persamaan kuadrat mempunyai sepasang akar kompleks bila Kedua akar kompleks tersebut biasanya dituliskan sebagai dengan menyatakan bilangan imajiner yang memenuhi…
Bilangan Negatif sebagai Pasangan Bilangan
Bila bilangan pecahan seperti melibatkan dua bilangan bulat, yaitu 1 dan 2, dan kemudian kita nyatakan sebagai pasangan bilangan bagaimana dengan bilangan negatif?…
Bilangan Pecahan sebagai Pasangan Bilangan
Bilangan pecahan seperti dan melibatkan dua bilangan bulat. Secara umum, bilangan pecahan yang dikenal pula sebagai bilangan rasional adalah bilangan…