Ruang Bernorma-2

Hendra Gunawan

Pada akhir tahun 1990-an, yang juga merupakan akhir abad ke-20, saya mulai berkenalan dengan norma-2, dan melakukan penelitian tentang ruang bernorma-2. Hasil penelitian pertama tentang topik ini saya tulis bersama dengan Prof. Wono Setya-Budhi dan papernya kami publikasikan di Majalah Ilmiah Himpunan Matematika Indonesia Vol. 6 (2000).

Bila saya baca kembali paper tersebut, saya sendiri merasa geli – mengapa saya kok mikirnya ruwet banget saat itu. Maklum, baru kenal dengan norma-2. Sekarang, setelah 18 tahun mengenalnya, saya bisa menjelaskan topik ini dengan lebih mudah. (Tetapi Anda tetap harus menyiapkan pensil dan kertas untuk mengikutinya.)

Misalkan X adalah ruang vektor real berdimensi d\ge 2. Pemetaan \|\cdot,\cdot\| : X \times X \to {\bf R} yang bersifat:

  1. \|x,y\| \ge 0 dan \|x,y\|=0 jika dan hanya jika x dan y bergantung linear,
  2. \|x,y\|=\|y,x\| untuk setiap x,y\in X,
  3. \|\alpha x,y\|=|\alpha|\,\|x,y\| untuk setiap x,y\in X dan \alpha \in {\bf R},
  4. \|x+y,z\|\le \|x,z\|+\|y,z\| untuk setiap x,y,z\in Z,

disebut norma-2 pada X, dan pasangan (X,\|\cdot,\cdot\|) disebut ruang bernorma-2.

Sebagai contoh, jika X dilengkapi dengan hasil kali dalam \langle\cdot,\cdot\rangle, maka pemetaan

\|x,y\|:=\bigl(\langle x,x\rangle \langle y,y\rangle-\langle x,y\rangle^2\bigr)^{1/2}

merupakan norma-2 pada X. Secara geometri, \|x,y\| di sini dapat diinterpretasikan sebagai luas jajaran genjang yang direntang oleh vektor x dan y.

Sifat 1 s/d 3 mudah diperiksa. Yang tidak terlalu mudah adalah Sifat 4, yang tak lain merupakan ketaksamaan segitiga untuk norma-2.

Untuk membuktikannya, perhatikan bahwa pemetaan \langle \cdot,\cdot|\cdot\rangle : X\times X\times X \to {\bf R} yang didefinisikan dengan rumus

\langle x,y|z\rangle := \langle x,y\rangle\langle z,z\rangle - \langle x,z\rangle \langle z,y\rangle

merupakan hasil kali dalam-2 pada X, yang bersifat:

  1. \langle x,x|z\rangle \ge 0 dan \langle x,x|z\rangle = 0 jika dan hanya jika x dan z bergantung linear,
  2. \langle x,x|z\rangle = \langle z,z|x\rangle untuk setiap x,z\in X,
  3. \langle x,y|z\rangle = \langle y,x|z\rangle untuk setiap x,y,z\in X,
  4. \langle \alpha x,y|z\rangle = \alpha \langle x,y|z\rangle untuk setiap x,y,z\in X dan \alpha \in {\bf R},
  5. \langle x_1+x_2,y|z\rangle = \langle x_1,y|z\rangle + \langle x_2,y|z\rangle untuk setiap x_1,x_2,y,z\in X.

Nah, dapat Anda periksa bahwa hasil kali dalam-2 di atas memenuhi ketaksamaan Cauchy-Schwarz:

\langle x,y|z\rangle^2 \le \langle x,x|z\rangle \langle y,y|z\rangle

untuk setiap x,y,z\in X. Selanjutnya, dengan menggunakan ketaksamaan Cauchy-Schwarz ini, tidak terlalu sulit bagi kita untuk membuktikan bahwa \|x,y\|:=\langle x,x|y\rangle^{1/2} memenuhi ketaksamaan segitiga (sila coba).

*

Bandung, 18-08-2018

Published by Hendra Gunawan

I'm a professor of mathematics at the Faculty of Mathematics and Natural Sciences, Bandung Institute of Technology, Bandung, Indonesia.

9 Comments

  1. Kebetulan saya sedang mempelajari ruang bernorma, jadi sangat terbantu dengan artikel ini 🙂
    Sambil mampir ke blog ini, saya coba buktikan hasil kali dalam-2 memenuhi ketaksamaan Cauchy-Schwarz.

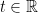    Untuk setiap x, y, z \in X dan t\in\mathbb{R}, definisikan fungsi y(t)=\left\langle tx+y,tx+y|z\right\rangle . Berdasarkan sifat 1, maka
    y(t)=\left\langle tx+y,tx+y|z\right\rangle \geq 0
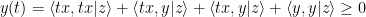
    Lebih lanjut dapat dituliskan
    y(t)=\left\langle tx, tx|z\right\rangle +\left\langle tx, y|z\right\rangle +\left\langle y, tx|z\right\rangle +\left\langle y, y|z\right\rangle \geq 0
    Berdasarkan sifat 3, maka
    y(t)= \left\langle tx, tx|z\right\rangle +\left\langle tx, y|z\right\rangle +\left\langle tx, y|z\right\rangle +\left\langle y, y|z\right\rangle \geq 0
    Kemudian kita terapkan sifat 4 untuk memperoleh

    y(t)=t^{2}\left\langle x, x|z\right\rangle +2t\left\langle x,y|z\right\rangle+\left\langle y, y|z\right\rangle \geq 0
    Perhatikan bahwa y(t)\geq 0 memiliki paling banyak satu solusi. Akibatnya diskriminan dari y(t) mestilah kurang dari atau sama dengan nol, dituliskan
    4t^{2}\left\langle x, y|z\right\rangle ^{2}-4t^{2}\left\langle x, x|z\right\rangle \left\langle y, y|z\right\rangle\leq 0
    Jadi
    \left\langle x, y|z\right\rangle ^{2}\leq \left\langle x, x|z\right\rangle \left\langle y, y|z\right\rangle.
    Terbukti.

    Like

    Reply

      1. Saya belum kepikiran untuk cara lainnya. Barangkali Prof Hendra berkenan untuk membagikannya di sini 🙂

        Like

      2. selamat siang bapak hendra, mohon maaf sebelumnya. saya ingin bertanya, untuk asal usul pendefinisian dari norm-2 itu dapat dari mana nggih pak? apakah ada kemungkinan untuk di definisikan yang lain? . terimakasih pak hendra

        Like

  2. Pingback: Ketaksamaan Cauchy-Schwarz dan Determinan Gram – Bermatematika
  3. Pingback: Norma di Ruang Bernorma-2 – Bermatematika
  4. Pingback: Ruang Bernorma-n – Bermatematika
  5. Pingback: Dua Norma Ekuivalen di Ruang Barisan l^p – Bermatematika

Leave a Reply

Fill in your details below or click an icon to log in:

Gravatar
WordPress.com Logo

You are commenting using your WordPress.com account. ( Log Out /  Change )

Twitter picture

You are commenting using your Twitter account. ( Log Out /  Change )

Facebook photo

You are commenting using your Facebook account. ( Log Out /  Change )

Cancel

Connecting to %s