Masih ingat deret teleskopis di bawah ini kan?
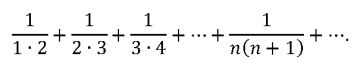
Nah, Gottfried Willhem Leibniz (1646-1716), sang penemu Kalkulus, ‘membuktikan’ bahwa deret ini konvergen ke 1 sebagai berikut:
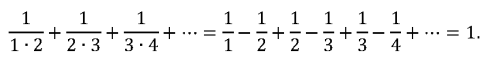
Betul kan? Hmm… tetapi kita juga mempunyai
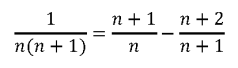
untuk setiap n = 1, 2, 3, …, sehingga
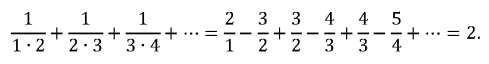
Oops! Apa yang salah?
*
Bandung, 01-06-2016

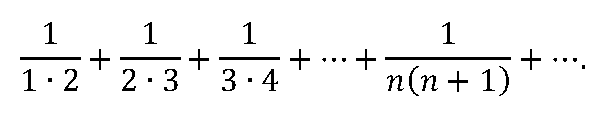
deret 1 + 1/n dan 1 + 1/(n+1) divergen
LikeLike
@stephanus tapi deret tersebut kan nanti dikurangi, penjumlahan (pengurangan) dua deret divergen belum tentu divergen juga…
LikeLike
Selisih dua deret divergen bisa saja konvergen.
LikeLike
Untuk permasalahan di atas pak, menurut saya yang membuat salah adalah ujung dari deret ke 2. Seharusnya ujung dari deret ke 2 konvergen menuju 1 sehingga 2-1=1, betul tidak pak?
LikeLike
Ya, betul. Kalau mau lebih aman, gunakan definisi.
LikeLike
lebih umum, jika deret $x_n$ konvergen ke $S$, maka deret $1+x_n-1$ konvergen ke $1+S$ dengan argumen serupa?
LikeLike