Segitiga Sama Sisi Terbesar dalam Persegi

Hendra Gunawan

Bila Anda mengikuti artikel dan problem di blog ini sejak awal, Anda mungkin masih ingat masalah menentukan persegi terkecil yang memuat segitiga sama sisi dengan panjang sisi 1 satuan panjang.

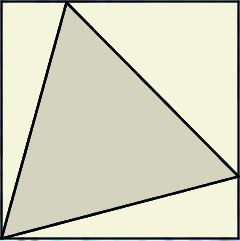
Nah, masalah dualnya adalah: diberikan persegi dengan panjang sisi 1 satuan panjang, tentukan segitiga sama sisi terbesar yang termuat dalam persegi tersebut.

Buktikan bahwa segitiga sama sisi terbesar yang termuat dalam persegi tersebut memiliki panjang sisi s=\sqrt{6}-\sqrt{2}.

*

Bandung, 30-06-2018

Unknown's avatar

Published by Hendra Gunawan

I'm a professor of mathematics at the Faculty of Mathematics and Natural Sciences, Bandung Institute of Technology, Bandung, Indonesia.

2 Comments

  1. Misalkan a menyatakan tinggi segitiga siku-siku di bawah segitiga sama-sisi, dan s merupakan sisi dari segitiga sama-sisi. Berdasarkan dalil Pythagoras kita punya

    s^{2}=(1-a)^{2}+(1-a)^{2}=2(1-a)^{2}=2a^{2}-4a+2    (pers 1)

    di lain pihak kita juga punya

    s^{2}=1^{2}+a^{2}=1+a^{2}    (pers 2)

    Kombinasikan pers 1 dan pers 2 untuk menghasilkan

    2a^{2}-4a+2=1+a^{2}

    a^{2}-4a+1=0

    Nilai a yang memenuhi adalah a=2-\sqrt{3}. Substitusikan nilai a ke dalam pers 2, sehingga diperoleh

    s^{2}=1+(2-\sqrt{3})^{2}=8-4\sqrt{3}=8-2\sqrt{2}\sqrt{6}=(\sqrt{6})^{2}-2\sqrt{2}\sqrt{6}+(\sqrt{2})^{2}=(\sqrt{6}-\sqrt{2})^{2}

    Nilai s yang memenuhi adalah s=\sqrt{6}-\sqrt{2}.

    Jadi segitiga sama sisi terbesar yang termuat dalam persegi tersebut memiliki panjang sisi s=\sqrt{6}-\sqrt{2}.

    Like

    Reply

Leave a comment