Masih ingat problem menentukan ukuran tabung paling ekonomis yang diunggah di blog ini dua tahun yang lalu?

Problem atau masalah ini merupakan Masalah Nilai Ekstrem dengan kendala: Diberikan luas permukaannya, tentukan volume maksimum. Masalah dualnya adalah: Diberikan volumenya, tentukan luas permukaan minimum.
Rumus volume tabung adalah dengan r menyatakan jari-jari tabung dan t menyatakan tinggi tabung. Luas permukaannya adalah
Jadi, untuk mendapatkan ukuran tabung paling ekonomis, Anda dapat menyelesaikan masalah optimisasi berikut:
(A) Diketahui tentukan nilai maksimum dari
Sebagai alternatif, Anda dapat menyelesaikan masalah optimisasi berikut:
(B) Diketahui tentukan nilai minimum dari
Dengan menyelesaikan masalah optimisasi (A) atau (B), buktikan bahwa tabung paling ekonomis adalah tabung yang memiliki tinggi sama dengan diameternya.
*
Bandung, 19-02-2018


Saya coba selesaikan masalah optimisasi (B). dan luas permukaannya
dan luas permukaannya  .
.
![A=2\pi r^{2}+\pi rt+\pi rt\geq 3\sqrt[3]{2\pi r^{2}\cdot\pi rt\cdot\pi rt}=3\sqrt[3]{2\pi(\pi^{2}r^{4}t^{2})}=3\sqrt[3]{2\pi V^{2}}](https://s0.wp.com/latex.php?latex=A%3D2%5Cpi+r%5E%7B2%7D%2B%5Cpi+rt%2B%5Cpi+rt%5Cgeq+3%5Csqrt%5B3%5D%7B2%5Cpi+r%5E%7B2%7D%5Ccdot%5Cpi+rt%5Ccdot%5Cpi+rt%7D%3D3%5Csqrt%5B3%5D%7B2%5Cpi%28%5Cpi%5E%7B2%7Dr%5E%7B4%7Dt%5E%7B2%7D%29%7D%3D3%5Csqrt%5B3%5D%7B2%5Cpi+V%5E%7B2%7D%7D&bg=%23ffffff&fg=%23000000&s=0&c=20201002)
Diberikan volume tabung sebagai
Berdasarkan ketaksamaan RA-RG kita punya
Kesamaan terjadi jika dan hanya jika , dengan
, dengan  . Kita peroleh
. Kita peroleh 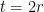 . Jadi nilai minimum dari
. Jadi nilai minimum dari 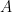 dicapai ketika panjang tinggi dan diameternya sama, yaitu
dicapai ketika panjang tinggi dan diameternya sama, yaitu
LikeLike
Akan lebih baik bila jawabannya dinyatakan dalam V, karena nilai V lah yang diberikan.
LikeLike
Sekarang saya akan selesaikan masalah optimisasi (A) dengan menggunakan metode pengali Lagrange. Fungsi yang akan dimaksimumkan adalah dengan kendala
dengan kendala  . Kita punya fungsi bantuannya sebagai
. Kita punya fungsi bantuannya sebagai
Turunkan fungsi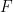 terhadap
terhadap  dan juga terhadap
dan juga terhadap 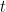 untuk memperoleh
untuk memperoleh
Berdasarkan nilai-nilai yang diperoleh, maka didapat persamaan
yang diperoleh, maka didapat persamaan
Jadi tabung paling ekonomis dicapai ketika panjang tinggi sama dengan diameternya.
LikeLike
Mantap! Terima kasih sudah menyelesaikan problem ini. Salam, HG
LikeLike