Fungsi f(x) = sinc x kontinu di 0 karena ketika x menuju 0, sinc x menuju f(0), yaitu 1. Fakta ini diperoleh dengan bantuan Prinsip Apit, mengingat cos x ≤ sinc x ≤ 1 untuk x di sekitar 0 (lihat gambar), dan cos x menuju 1 bila x menuju 0.

O ya, Prinsip Apit menyatakan jika suatu fungsi diapit oleh dua fungsi lain, dan kedua fungsi pengapitnya memiliki limit yang sama di suatu titik, maka fungsi yang diapit tadi akan memiliki limit yang sama di titik tersebut.
Persisnya, misalkan f(x) ≤ g(x) ≤ h(x) untuk x di sekitar c. Prinsip Apit berbunyi:
![]()
Nah, pada kasus di atas, f(x) = cos x, g(x) = sinc x, dan h(x) = 1, dengan c = 0 dan L = 1.
Dengan Prinsip Apit pula, kita dapat membuktikan bahwa sinc x menuju 0 bila x menuju tak terhingga, mengingat untuk setiap x > 0 kita mempunyai
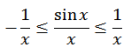
dan 1/x menuju 0 bila x menuju tak terhingga. (Serupa dengan itu, sinc x menuju 0 bila x menuju minus tak terhingga.)
Jadi, dengan Prinsip Apit, kita telah membuktikan
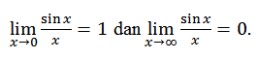
Pengetahuan tentang limit sinc x di 0 dipakai antara lain untuk membuktikan bahwa turunan dari sin x adalah cos x.
*
Bandung, 07-02-2017

