Fungsi Kompleks f(z)=1/z

Hendra Gunawan

Saya telah memperkenalkan fungsi kompleks dan memberikan contoh fungsi kompleks f(z)=\frac{1}{z},\ z\not=0. Fungsi ini memetakan lingkaran satuan S:=\{z\,:\,|z|=1\} ke lingkaran satuan lagi. Persisnya, f memetakan z\in S ke \bar{z}, karena

\frac{1}{z}=\frac{\bar{z}}{|z|^2}=\bar{z},

untuk setiap z\in S.

Untuk z lainnya, kita amati bahwa

\Bigl|\frac{1}{z}\Bigr|=\frac{|\bar{z}|}{|z|^2}=\frac{1}{|z|}.

Dari sinilah kita bisa menyimpulkan bahwa fungsi f(z)=\frac{1}{z} memetakan titik yang berada di dekat 0 ke titik yang berada jauh dari 0.

Selain itu, apa lagi yang dapat kita katakan tentang fungsi f(z)=\frac{1}{z}?

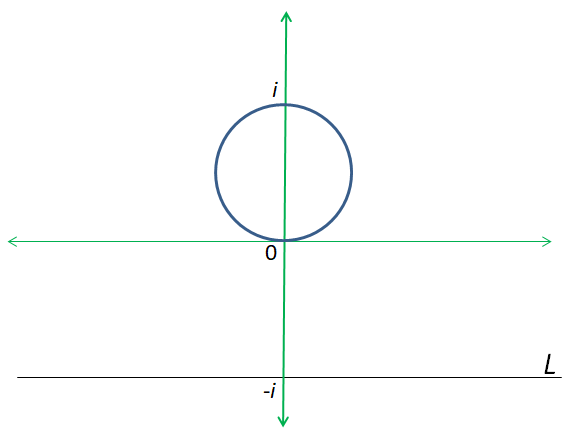
Dalam pembahasan fungsi kompleks, kita kadang ingin mengetahui apakah fungsi tersebut memetakan lingkaran ke lingkaran, lingkaran ke garis, garis ke lingkaran, atau garis ke garis. Tentu tidak selalu mudah memeriksa hal ini. Namun, sebagai contoh, kita dapat memeriksa bahwa fungsi f(z)=\frac{1}{z} memetakan lingkaran ‘terputus’ C:=\{z=x+iy\,:\,x^2+(y-\frac12)^2=\frac14\}\setminus\{0\} ke garis L:=\{w=a-i\,:\,a\in\mathbb{R}\}.

Perhatikan bahwa untuk z\not=0, kita mempunyai

w:=\frac{1}{z}=\frac{1}{x+iy}=\frac{x}{x^2+y^2}-\frac{y}{x^2+y^2}i.

Khususnya, untuk z=x+iy\in C, kita mempunyai x^2+y^2=y, sehingga kita peroleh

w=\frac{x}{y}-i,

dengan y\not=0. Catat bahwa \frac{x}{y} dapat bernilai bilangan real sembarang.

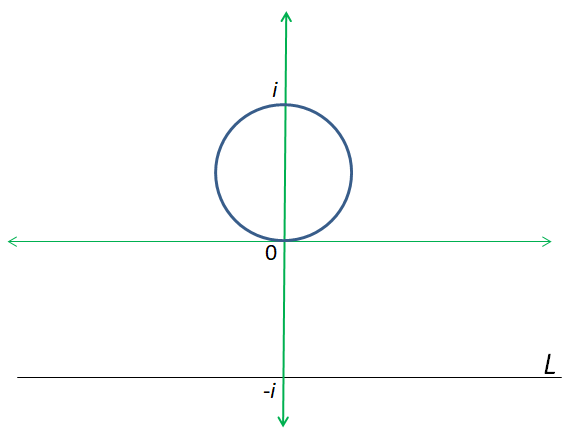
Dalam hal ini, himpunan \{w=\frac{1}{z}\,:\,z\in C\} membentuk garis yang melalui bilangan -i pada sumbu imajiner.

*

Bandung, 23-06-2020

Unknown's avatar

Published by Hendra Gunawan

I'm a professor of mathematics at the Faculty of Mathematics and Natural Sciences, Bandung Institute of Technology, Bandung, Indonesia.

Leave a comment