Problem (mudah): Buktikan bahwa bukan merupakan fungsi Lipschitz pada
Catatan. Pada artikel sebelumnya, kita telah membahas bahwa fungsi Lipschitz pada interval I pasti kontinu seragam pada I. Fungsi merupakan contoh yang memperlihatkan bahwa fungsi yang kontinu seragam pada I tidak harus memenuhi kondisi Lipschitz pada I. [O ya, fungsi yang kontinu pada interval tutup dan terbatas senantiasa kontinu seragam pada interval tersebut.]
*
Bandung, 22-05-2018


Andaikan fungsi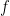 merupakan fungsi Lipschitz pada
merupakan fungsi Lipschitz pada ![I = [0,1]](https://s0.wp.com/latex.php?latex=I+%3D+%5B0%2C1%5D+&bg=%23ffffff&fg=%23000000&s=0&c=20201002) , maka terdapat
, maka terdapat  sedemikian sehingga
sedemikian sehingga  untuk setiap
untuk setiap 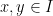 . Menurut sifat Archimedes terdapat
. Menurut sifat Archimedes terdapat 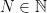 sedemikian sehingga
sedemikian sehingga 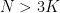 . Pilih
. Pilih 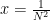 dan
dan 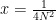 . Maka kita peroleh
. Maka kita peroleh  .
.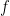 bukan merupakan fungsi Lipschitz pada
bukan merupakan fungsi Lipschitz pada 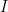 .
.
Kontradiksi. Jadi mestilah
[QED]
LikeLike
Maaf ada kesalahan pada jawaban sebelumnya.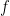 merupakan fungsi Lipschitz pada
merupakan fungsi Lipschitz pada ![I = [0,1]](https://s0.wp.com/latex.php?latex=I+%3D+%5B0%2C1%5D+&bg=%23ffffff&fg=%23000000&s=0&c=20201002) , maka terdapat
, maka terdapat  sedemikian sehingga
sedemikian sehingga  untuk setiap
untuk setiap 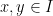 . Menurut sifat Archimedes terdapat
. Menurut sifat Archimedes terdapat 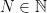 sedemikian sehingga
sedemikian sehingga 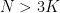 . Pilih
. Pilih 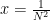 dan
dan  . Maka kita peroleh
. Maka kita peroleh  .
.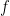 bukan merupakan fungsi Lipschitz pada
bukan merupakan fungsi Lipschitz pada 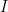 .
.
Andaikan fungsi
Kontradiksi. Jadi mestilah
[QED] TERBUKTI
LikeLike
Andaikan fungsi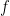 merupakan fungsi Lipschitz pada
merupakan fungsi Lipschitz pada ![I = [0,1]](https://s0.wp.com/latex.php?latex=I+%3D+%5B0%2C1%5D+&bg=%23ffffff&fg=%23000000&s=0&c=20201002) , maka terdapat
, maka terdapat  sedemikian sehingga
sedemikian sehingga  untuk setiap
untuk setiap 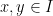 . Menurut sifat Archimedes terdapat
. Menurut sifat Archimedes terdapat 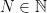 sedemikian sehingga
sedemikian sehingga 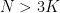 . Pilih
. Pilih 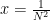 dan
dan  . Maka kita peroleh
. Maka kita peroleh  .
.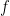 bukan merupakan fungsi Lipschitz pada
bukan merupakan fungsi Lipschitz pada 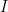 .
.
Kontradiksi. Jadi mestilah
[QED]
LikeLike